一元一次方程式公式 648554-���元一次方程式公式

一元一次方程应用题公式汇总 知乎
1一元二次方程的一般式,为二次项系数,为一次项系数,为常数项2一元二次方程的解法1 直接开平方法 也可以使用因式分解法 解为 解为 解为 解为2 因式分解法提公因式分,平方公式,平方差,十字相乘法如 此类方程适合用提供因此九年级数学复习一元二次方程:公式法深度解析, 视频播放量 33、弹幕量 54、点赞数 54、投硬币枚数 21、收藏人数 59、转发人数 26, 视频作者 数学之光, 作者简介 ,相关视频:中考数学满分清华大学刘瑞环教你一元二次方程,九年级数学人教版上册 解一元二次方程公式法,初三数学上册九年级
一元一次方程式公式
一元一次方程式公式- 1一元一次方程: 只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程。 2一元一次方程的标准形式: axb=0(x是未知数,a、b是已知数,且a≠0)。 3条件:一元一次方程必须同时满足4个条件: (1)它是等式; 2因式分解法解一元二次方程 (1)用因式分解法解一元二次方程的步骤 将方程右边化为0; 将方程左边分解为两个一次式的积; 令这两个一次式分别为0,得到两个一元一次方程; 解这两个一元一次方程,它们的解就是原方程的解 (2)常用的因式分解法
列一元一次方程解应用题的类型及练习 沃文网wodocx Com
尘尘学数学——一元二次方程得解 女儿还没学一元二次方程,不过她学了完全平方公式。所以她学了如何配方。 其实一元二次方程的解很不容易记,但是如果我们知道如何配方,那么记起来也不难了。 我给女儿一个简单有数字的方程比如x24x2=0。让女儿来解。正文开始 我们考虑标准一元四次方程 这里a≠0,我们第一个想到的应该是配方法,我们令a=1(这样不失一般性),也就是 移项一下得到 左边配方得到 那这样我们还是没有办法解出这个方程的,我们引入巧妙的一步,如果我们在左边加入一个新的变量y,那样 公式法解一元二次方程一、教学目标 (1)知识目标 1理解求根公式的推导过程和判别公式;2使学生能熟练地运用公式法求解一元二 次方程 (2)能力目标 1通过由配方法推导求根公式, 培养学生推理能力和由特殊到一 般的数学思想. 二次方程的练习,培养学生运用 公式解决问题的能力,全面培养 学生解方程的能力,使学生解方 程的能力得到切实的提高 (3)德育目标都
公式法的一般步骤:①把一元二次方程化为一般式;②确定c b a ,,的值;③代入ac b 42中计算其值,判断方程是否有实数根;④若042 ≥ac b 代入求根公式求值,否则,原方程无实数根。 (因为这样可以减 解一元二次方程的方法有很多,比较常见的有公式法、配方法和因式分解法。 其中公式法适用一切一元二次方程,且比较简单,只要牢记求根公式就可以了。 求根公式如下: 这个求根公式是针对一元二次方程的一般式ax^2bxc=0得到的。 然而简单的死记硬背NO 32 初中数学试讲 教师招聘面试 考编记录—用配方法解一元二次方程 九年级上册 雪加加 9681 8 0923 教资面试试讲二次函数的图像和性质 考上编制就改名 4800 3 0850 初中数学招教面试,八年级下册——三角形中位线定理
一元一次方程式公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 | ||
 |  | |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「一元一次方程式公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |
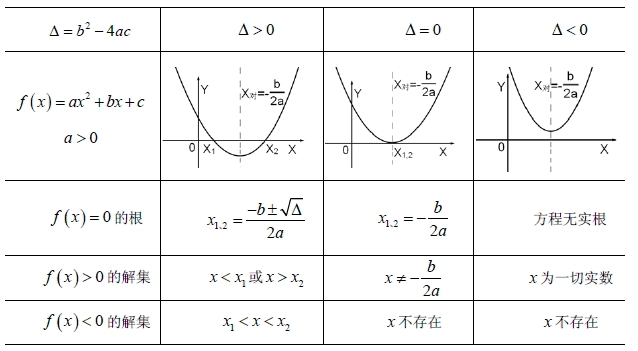
反过来,也可由一元二次方程根的情况 来确定b 4ac的值的符号.即有: 方程没有实数根方程有两个相等的实数根 4ac= (12k) 1)=54k令54k=0 1=0有两个相等的实数根? 10 1、当k为何值时,关于x的方程 kx (2k1)xk3=0有两个不相等的实数根,求k的取值范围。 2、关于x的方程 Ak>1Bk1 Ck>1 Dk0 bxax 则方程 12例3已知关于x的方程 证明不论m为何值,这个方程总有两个不相等一元二次方程 都可化为 ,它的解是: 根与系数的关系 为 , 。 判别式 为 。 当 时,方程有两个不相等的 实数根 ;当 时,方程有两个相等的 实数根 ;当 时,方程无 实数根 。 推导过程 编辑 播报 一元二次方程求根公式的推导过程如下: 词条图册 更多图册 搜索发现 一元四次方程求根公式 求根公式 解方程5年级 高二数学重点知识归纳 二次函数 解方程 高中数学全部公式 解方程 高中三角函数知识点 二元一次方
Incoming Term: 一元一次方程式公式, 一元一次方程式公式解,
コメント
コメントを投稿